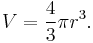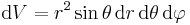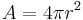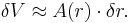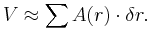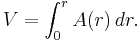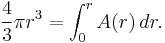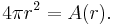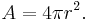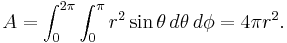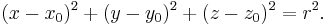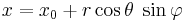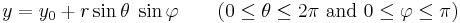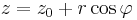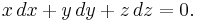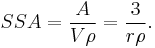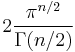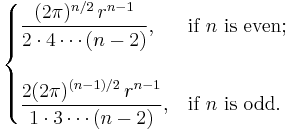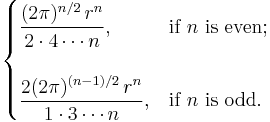Sphere
A sphere (from Greek σφαῖρα — sphaira, "globe, ball"[1]) is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point. This distance r is known as the radius of the sphere. The maximum straight distance through the sphere is known as the diameter of the sphere. It passes through the center and is thus twice the radius.
In mathematics, a careful distinction is made between the sphere (a two-dimensional spherical surface embedded in three-dimensional Euclidean space) and the ball (the three-dimensional shape consisting of a sphere and its interior).
Volume of a sphere
In 3 dimensions, the volume inside a sphere (that is, the volume of a ball) is given by the formula
where r is the radius of the sphere and π is the constant pi. This formula was first derived by Archimedes, who showed that the volume of a sphere is 2/3 that of a circumscribed cylinder. (This assertion follows from Cavalieri's principle.) In modern mathematics, this formula can be derived using integral calculus, i.e. disk integration to sum the volumes of an infinite number of circular disks of infinitesimal thickness stacked centered side by side along the x axis from x = 0 where the disk has radius r (i.e. y = r) to x = r where the disk has radius 0 (i.e. y = 0).
At any given x, the incremental volume (δV) is given by the product of the cross-sectional area of the disk at x and its thickness (δx):
The total volume is the summation of all incremental volumes:
In the limit as δx approaches zero[2] this becomes:
At any given x, a right-angled triangle connects x, y and r to the origin, hence it follows from Pythagorean theorem that:
Thus, substituting y with a function of x gives:
This can now be evaluated:
Therefore the volume of a sphere is:
Alternatively this formula is found using spherical coordinates, with volume element
In higher dimensions, the sphere (or hypersphere) is usually called an n-ball. General recursive formulas exist for deriving the volume of an n-ball.
For most practical purposes, the volume of a sphere inscribed in a cube can be approximated as 52.4% of the volume of the cube, since 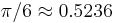 . For example, since a cube with edge length 1 m has a volume of 1 m3
. For example, since a cube with edge length 1 m has a volume of 1 m3
, a sphere with diameter 1 m has a volume of about 0.524 m3
.
Surface area of a sphere
The surface area of a sphere is given by the following formula.
This formula was first derived by Archimedes, based upon the fact that the projection to the lateral surface of a circumscribing cylinder (i.e. the Lambert cylindrical equal-area projection) is area-preserving. It is also the derivative of the formula for the volume with respect to r because the total volume of a sphere of radius r can be thought of as the summation of the surface area of an infinite number of spherical shells of infinitesimal thickness concentrically stacked inside one another from radius 0 to radius r. At infinitesimal thickness the discrepancy between the inner and outer surface area of any given shell is infinitesimal and the elemental volume at radius r is simply the product of the surface area at radius r and the infinitesimal thickness.
At any given radius r, the incremental volume (δV) is given by the product of the surface area at radius r (A(r)) and the thickness of a shell (δr):
The total volume is the summation of all shell volumes:
In the limit as δr approaches zero[2] this becomes:
Since we have already proved what the volume is, we can substitute V:
Differentiating both sides of this equation with respect to r yields A as a function of r:
Which is generally abbreviated as:
Alternatively, the area element on the sphere is given in spherical coordinates by 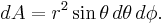 . With Cartesian coordinates, the area element
. With Cartesian coordinates, the area element 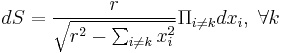 . More generally, see area element.
. More generally, see area element.
The total area can thus be obtained by integration:
Equations in R3
In analytic geometry, a sphere with center (x0, y0, z0) and radius r is the locus of all points (x, y, z) such that
The points on the sphere with radius r can be parametrized via
(see also trigonometric functions and spherical coordinates).
A sphere of any radius centered at zero is an integral surface of the following differential form:
This equation reflects the fact that the position and velocity vectors of a point traveling on the sphere are always orthogonal to each other.
The sphere has the smallest surface area among all surfaces enclosing a given volume and it encloses the largest volume among all closed surfaces with a given surface area. For this reason, the sphere appears in nature: for instance bubbles and small water drops are roughly spherical, because the surface tension locally minimizes surface area. The surface area in relation to the mass of a sphere is called the specific surface area. From the above stated equations it can be expressed as follows:
A sphere can also be defined as the surface formed by rotating a circle about any diameter. If the circle is replaced by an ellipse, and rotated about the major axis, the shape becomes a prolate spheroid, rotated about the minor axis, an oblate spheroid.
Terminology
Pairs of points on a sphere that lie on a straight line through its center are called antipodal points. A great circle is a circle on the sphere that has the same center and radius as the sphere, and consequently divides it into two equal parts. The shortest distance between two distinct non-antipodal points on the surface and measured along the surface, is on the unique great circle passing through the two points. Equipped with the great-circle distance, a great circle becomes the Riemannian circle.
If a particular point on a sphere is (arbitrarily) designated as its north pole, then the corresponding antipodal point is called the south pole and the equator is the great circle that is equidistant to them. Great circles through the two poles are called lines (or meridians) of longitude, and the line connecting the two poles is called the axis of rotation. Circles on the sphere that are parallel to the equator are lines of latitude. This terminology is also used for astronomical bodies such as the planet Earth, even though it is not spherical and only approximately spheroidal (see geoid).
Hemisphere
A sphere is divided into two equal hemispheres by any plane that passes through its center. If two intersecting planes pass through its center, then they will subdivide the sphere into four lunes or biangles, the vertices of which all coincide with the antipodal points lying on the line of intersection of the planes.
The antipodal quotient of the sphere is the surface called the real projective plane, which can also be thought of as the northern hemisphere with antipodal points of the equator identified.
The round hemisphere is conjectured to be the optimal (least area) filling of the Riemannian circle.
If the planes don't pass through the sphere's center, then the intersection is called spheric section.[4]
Generalization to other dimensions
Spheres can be generalized to spaces of any dimension. For any natural number n, an n-sphere, often written as Sn, is the set of points in (n + 1)-dimensional Euclidean space which are at a fixed distance r from a central point of that space, where r is, as before, a positive real number. In particular:
- a 0-sphere is a pair of endpoints of an interval (−r, r) of the real line
- a 1-sphere is a circle of radius r
- a 2-sphere is an ordinary sphere
- a 3-sphere is a sphere in 4-dimensional Euclidean space.
Spheres for n > 2 are sometimes called hyperspheres.
The n-sphere of unit radius centred at the origin is denoted Sn and is often referred to as "the" n-sphere. Note that the ordinary sphere is a 2-sphere, because it is a 2-dimensional surface (which is embedded in 3-dimensional space).
The surface area of the (n − 1)-sphere of radius 1 is
where Γ(z) is Euler's Gamma function.
Another formula for surface area is
and the volume is the surface area times 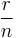 or
or
Generalization to metric spaces
More generally, in a metric space (E,d), the sphere of center x and radius r > 0 is the set of points y such that d(x,y) = r.
If the center is a distinguished point considered as origin of E, as in a normed space, it is not mentioned in the definition and notation. The same applies for the radius if it is taken equal to one, as in the case of a unit sphere.
In contrast to a ball, a sphere may be an empty set, even for a large radius. For example, in Zn with Euclidean metric, a sphere of radius r is nonempty only if r2 can be written as sum of n squares of integers.
Topology
In topology, an n-sphere is defined as a space homeomorphic to the boundary of an (n+1)-ball; thus, it is homeomorphic to the Euclidean n-sphere, but perhaps lacking its metric.
- a 0-sphere is a pair of points with the discrete topology
- a 1-sphere is a circle (up to homeomorphism); thus, for example, (the image of) any knot is a 1-sphere
- a 2-sphere is an ordinary sphere (up to homeomorphism); thus, for example, any spheroid is a 2-sphere
The n-sphere is denoted Sn. It is an example of a compact topological manifold without boundary. A sphere need not be smooth; if it is smooth, it need not be diffeomorphic to the Euclidean sphere.
The Heine-Borel theorem implies that a Euclidean n-sphere is compact. The sphere is the inverse image of a one-point set under the continuous function ||x||. Therefore, the sphere is closed. Sn is also bounded; therefore it is compact.
Spherical geometry
The basic elements of Euclidean plane geometry are points and lines. On the sphere, points are defined in the usual sense, but the analogue of "line" may not be immediately apparent. If one measures by arc length one finds that the shortest path connecting two points lying entirely in the sphere is a segment of the great circle containing the points; see geodesic. Many theorems from classical geometry hold true for this spherical geometry as well, but many do not (see parallel postulate). In spherical trigonometry, angles are defined between great circles. Thus spherical trigonometry is different from ordinary trigonometry in many respects. For example, the sum of the interior angles of a spherical triangle exceeds 180 degrees. Also, any two similar spherical triangles are congruent.
Eleven properties of the sphere
In their book Geometry and the imagination[5] David Hilbert and Stephan Cohn-Vossen describe eleven properties of the sphere and discuss whether these properties uniquely determine the sphere. Several properties hold for the plane which can be thought of as a sphere with infinite radius. These properties are:
- The points on the sphere are all the same distance from a fixed point. Also, the ratio of the distance of its points from two fixed points is constant.
- The first part is the usual definition of the sphere and determines it uniquely. The second part can be easily deduced and follows a similar result of Apollonius of Perga for the circle. This second part also holds for the plane.
- The contours and plane sections of the sphere are circles.
- This property defines the sphere uniquely.
- The sphere has constant width and constant girth.
- The width of a surface is the distance between pairs of parallel tangent planes. There are numerous other closed convex surfaces which have constant width, for example the Meissner body. The girth of a surface is the circumference of the boundary of its orthogonal projection on to a plane. It can be proved that each of these properties implies the other.
- All points of a sphere are umbilics.
- At any point on a surface we can find a normal direction which is at right angles to the surface, for the sphere these are the lines radiating out from the center of the sphere. The intersection of a plane containing the normal with the surface will form a curve called a normal section and the curvature of this curve is the sectional curvature. For most points on most surfaces, different sections will have different curvatures; the maximum and minimum values of these are called the principal curvatures. It can be proved that any closed surface will have at least four points called umbilical points. At an umbilic all the sectional curvatures are equal; in particular the principal curvatures are equal. Umbilical points can be thought of as the points where the surface is closely approximated by a sphere.
- For the sphere the curvatures of all normal sections are equal, so every point is an umbilic. The sphere and plane are the only surfaces with this property.
- The sphere does not have a surface of centers.
- For a given normal section there is a circle whose curvature is the same as the sectional curvature, is tangent to the surface and whose center lines along on the normal line. Take the two centers corresponding to the maximum and minimum sectional curvatures: these are called the focal points, and the set of all such centers forms the focal surface.
- For most surfaces the focal surface forms two sheets each of which is a surface and which come together at umbilical points. There are a number of special cases. For channel surfaces one sheet forms a curve and the other sheet is a surface; For cones, cylinders, toruses and cyclides both sheets form curves. For the sphere the center of every osculating circle is at the center of the sphere and the focal surface forms a single point. This is a unique property of the sphere.
- All geodesics of the sphere are closed curves.
- Geodesics are curves on a surface which give the shortest distance between two points. They are a generalization of the concept of a straight line in the plane. For the sphere the geodesics are great circles. There are many other surfaces with this property.
- Of all the solids having a given volume, the sphere is the one with the smallest surface area; of all solids having a given surface area, the sphere is the one having the greatest volume.
- These properties define the sphere uniquely. These properties can be seen by observing soap bubbles. A soap bubble will enclose a fixed volume and due to surface tension its surface area is minimal for that volume. This is why a free floating soap bubble approximates a sphere (though external forces such as gravity will distort the bubble's shape slightly).
- The sphere has the smallest total mean curvature among all convex solids with a given surface area.
- The mean curvature is the average of the two principal curvatures and as these are constant at all points of the sphere then so is the mean curvature.
- The sphere has constant mean curvature.
- The sphere is the only imbedded surface without boundary or singularities with constant positive mean curvature. There are other immersed surfaces with constant mean curvature. The minimal surfaces have zero mean curvature.
- The sphere has constant positive Gaussian curvature.
- Gaussian curvature is the product of the two principal curvatures. It is an intrinsic property which can be determined by measuring length and angles and does not depend on the way the surface is embedded in space. Hence, bending a surface will not alter the Gaussian curvature and other surfaces with constant positive Gaussian curvature can be obtained by cutting a small slit in the sphere and bending it. All these other surfaces would have boundaries and the sphere is the only surface without boundary with constant positive Gaussian curvature. The pseudosphere is an example of a surface with constant negative Gaussian curvature.
- The sphere is transformed into itself by a three-parameter family of rigid motions.
- Consider a unit sphere placed at the origin, a rotation around the x, y or z axis will map the sphere onto itself, indeed any rotation about a line through the origin can be expressed as a combination of rotations around the three coordinate axis, see Euler angles. Thus there is a three-parameter family of rotations which transform the sphere onto itself, this is the rotation group, SO(3). The plane is the only other surface with a three-parameter family of transformations (translations along the x and y axis and rotations around the origin). Circular cylinders are the only surfaces with two-parameter families of rigid motions and the surfaces of revolution and helicoids are the only surfaces with a one-parameter family.
Cubes in relation to spheres
For every sphere there are multiple cuboids that may be inscribed within the sphere. When briefly considered it becomes apparent that the largest of the multiple cuboids which may be inscribed is a cube.
See also
References
- ^ σφαῖρα, Henry George Liddell, Robert Scott, A Greek-English Lexicon, on Perseus
- ^ a b Pages 141, 149. E.J. Borowski, J.M. Borwein. Collins Dictionary of Mathematics. ISBN 0-00-434347-6.
- ^ New Scientist | Technology | Roundest objects in the world created
- ^ Weisstein, Eric W., "Spheric section" from MathWorld.
- ^ Hilbert, David; Cohn-Vossen, Stephan (1952). Geometry and the Imagination (2nd ed.). Chelsea. ISBN 0-8284-1087-9.
- William Dunham. "Pages 28, 226", The Mathematical Universe: An Alphabetical Journey Through the Great Proofs, Problems and Personalities, ISBN 0-471-17661-3.
External links
- Calculate volume of sphere
- Sphere (PlanetMath.org website)
- Weisstein, Eric W., "Sphere" from MathWorld.
- Mathematica/Uniform Spherical Distribution
- Outside In. 2007-11-14. http://video.google.com/videoplay?docid=-6626464599825291409. Retrieved 2007-11-24. (computer animation showing how the inside of a sphere can turn outside.)
- Program in C++ to draw a sphere using parametric equation
- Surface area of sphere proof.
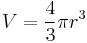
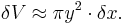
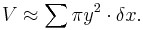
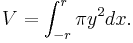
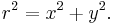
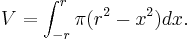
![\!V = \pi \left[r^2x - \frac{x^3}{3} \right]_{-r}^{r} = \pi \left(r^3 - \frac{r^3}{3} \right) - \pi \left(-r^3 %2B \frac{r^3}{3} \right) = \frac{4}{3}\pi r^3.](/2012-wikipedia_en_all_nopic_01_2012/I/eb0e94717b0e0c5b44f997df13d4fa4a.png)